In one of my last posts I puzzled over this section in Gravity’s Rainbow:

And what is the specific shape whose center of gravity is the Brennschluss Point? Don’t jump at an infinite number of possible shapes. There’s only one. It is most likely an interface between one order of things and another.

Pynchon, Thomas. Gravity’s Rainbow (Classic, 20th-Century, Penguin) (S.302). Penguin Publishing Group. Kindle-Version.

Some readers suggested that the shape in question might be “the parabola”, which makes sense because the rocket trajectory is similar to a parabola. But I’m not 100% satisfied with this solution. Let me explain why:

1. A parabola is not a specific shape, but a curve described by f(x) = a*x^2 where a != 0. So there are different kinds of parabolas having different widths.
2. For a parabola the Brennschlusspoint would never be the same as the center of gravity (see illustration below)

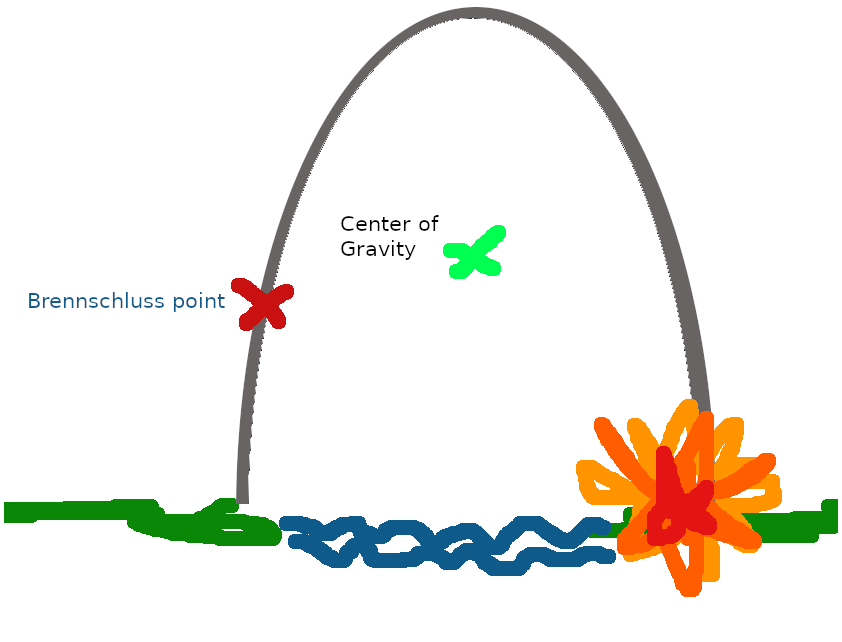
So what specific shape would work?

Let me explain with a Limerick:

There once was a fellow named Moritz

Who wanted to land a few more hits

But he had not enough sleep

He launched the rocket to steep

Everyone had to hide in the coal pits