Gravity’s Rainbow is one of those books I could devote my whole life to and still wouldn’t understand half of it. Many parts probably aren’t meant to be understood. Fortunately, there are also some math formulas:

For an excellent explanation of the formula’s origin and a discussion of its meaning within the context of the novel, take a look at this paper. The goal of this blog post is limited in scope in attempting an exploration of what those symbols actually do. This will be easier by consulting this diagram from the paper where Pynchon most likely got the formula from:

Let’s start with the right part of the equation, as the variable β stands for the angle of the rocket’s steering rudders. This is the only variable that can be controlled, and it’s what this formula is meant to calculate.

On the other side of the equation, ϕ is the difference between the rocket’s assigned path and its real path. This angle has an impact on the moments of inertia (first term) and the air resistance (second term). If it is big, more force is needed to correct the flight path.

The third term on the left side is about lateral forces, like a wind from the side, having the angle 90° + α relative to the missile. s1-s2 is the difference between the rocket’s aerodynamic centre and its gravitational centre. The more significant that difference is, the harder it is to control the yaw.

Let’s look at an example: Assume the rocket engineers at Peenemünde are launching a rocket that was carefully calibrated to land precisely on poor Slothrop’s head. But of course, Slothrop gets wind of this via his telepathic link to the V2 and runs away. Unfortunately for him, the rocket contains the S-Gerät, which adapts the flight path to hit him anyway. Another example of modern technology ruining the day.

Say the way in which the yaw is corrected follows the following formula:

ϕ(t) = 1/(t^3+1) – 0.5

(Don’t ask me why. The S-Gerät acts in mysterious ways)

The curve starts out with a mismatch between the assigned path and the real flight path that then gets gradually reduced to 0 at t=1:

The second and first derivatives of this formula are:

ϕ”(t) = (18 t^4)/(1 + t^3)^3 – (6 t)/(1 + t^3)^2

ϕ'(t) = -3t^2/(t^3+1)^2

To simplify matters, we will assume that there are no lateral forces and that the other variables are really constants with a value of 1. This means the formula simplifies to this:

ϕ”(t) + ϕ'(t) = -β

<=> β = – ϕ”(t) – ϕ'(t)

<=> β = – ϕ”(t) – ϕ'(t)

<=> β = -(18 t^4)/(1 + t^3)^3 + (6 t)/(1 + t^3)^2 + (3 t^2)/(1 + t^3)^2

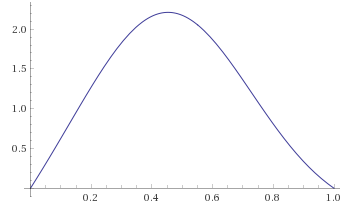
So the angle of the rudders will be gradually increased and then gradually decreased to control the yaw. Good to know?